Fraktály - snaha matematiky o narovnání přírody

Fraktál je geometrický objekt se zdánlivě složitou strukturou. Typickou vlastností je soběpodobnost, kdy je fraktální obrazec utvářen z částí, které jsou zmenšenými kopiemi celého obrazce.  

Matematika fraktálů je pokus se přiblížit zlomkovitosti každodenního života. Fraktální geometrie má obrovský význam při popisu tvarů a objektů reálného světa. 

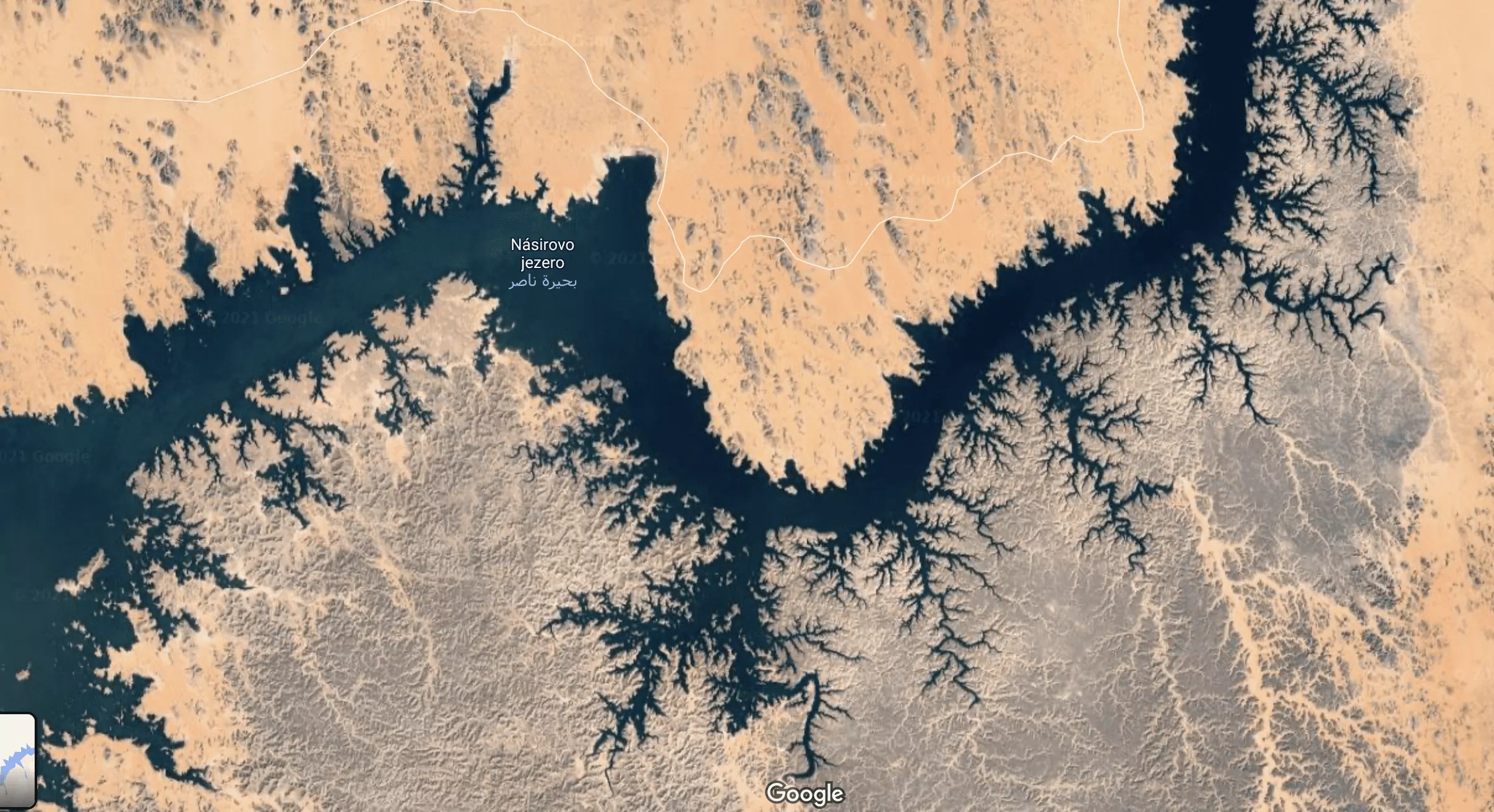
Většina skutečných objektů je příliš složitá na to, abychom je mohli popsat prostřednictvím eukleidovské geometrie, naproti tomu fraktální geometrie dokáže znázornit i velmi složité struktury, jakými jsou například vodní síť, strukturu plic, tvar mraků nebo elektrický výboj.  

I lidské tělo je složeno z fraktálů – každá úroveň zvětšení obsahuje detaily a celky. Například plíce neuvěřitelně efektivně naplňují prostor. Mají spoustu záhybů a vroubků, jejich objem je velmi malý, ale celkový povrch je enormní.  

Rostliny také rostou podle jednoduchých pravidel, ale nakonec dosáhnou velké komplexnosti. Kvůli spletitému povrchu brokolice je měření jeho plochy obtížné. Čím blíže se díváme na opakující se vzorce růžiček a závitů, tím více detailů vidíme. Metoda načítání opakovaných jednotek na různých úrovních měřítka, jak se jeví na romanescu (nejkrásnější zelenina na světě – „zelený květák“, dala vzniknout fenoménu zvanému „soběpodobnost“)

Jedním ze základních tvarů vyskytujících se ve fraktální geometrii je Kochova vločka, která byla poprvé popsána roku 1904. Na jejím tvaru si můžeme snadno vysvětlit princip vytváření fraktálů a vlastnost soběpodobnosti. Základem vločky je rovnostranný trojúhelník o délce jeden centimetr. Ke středům stran tohoto trojúhelníka připojíme další trojúhelníky zmenšené oproti předchozímu v poměru 1:3. K těmto trojúhelníkům připojíme další trojúhelníky opět zmenšené o jednu třetinu. Postupným opakováním tohoto postupu získáme členitý obrazec zvaný Kochova vločka.   

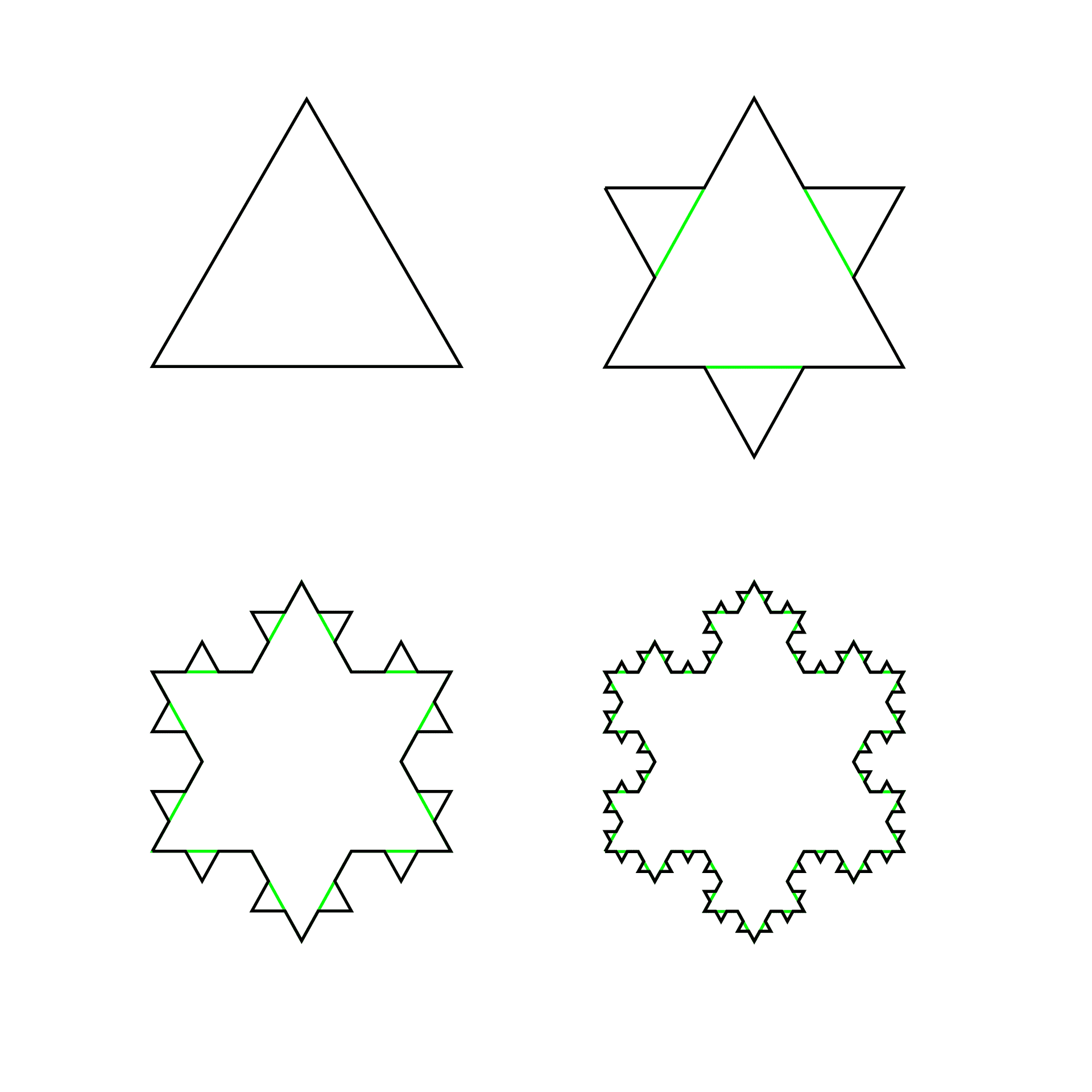
Dalším, kdo se touto oblastí zabýval, byl Belgický matematik Benoit Mandelbrot. V roce 1975 prosadil termín fraktál, aby charakterizoval novou geometrii, které je „v každém měřítku stejně syrová“. Na začátku stál jednoduchý problém týkající se měření pobřeží.  

Na mapě ve velkém měřítku je pobřeží nějakého ostrova velmi zjednodušené, protože není možné zobrazit detaily. Chceme-li získat větší detail, musíme si obraz přiblížit, spatřit a změřit přesnější hranice a získat přesnější odhad skutečné velikosti pobřeží. Takto lze postupovat dále, výpočet je vždy složitější a je nemožné dospět ke konečnému číslu dřív, než je okraj pevniny nerozeznatelný od vody.  

Mandelbrotova množina 

Mandelbrotova množina patří mezi nejčastěji zobrazované obrazy v moderní matematice. Poprvé se objevila až v 80. letech 20. století s rozvojem počítačoví techniky a jejím využíváním pro stále přesnější matematické výpočty. I když vypadá Mandelbrotova množina složitě, její výpočet není vůbec složitý a obsahuje jen sčítání a násobení.  

Vzorec pro její výpočet je z = z² + c. Klíčové vlastnost je iterace – jednoduché pravidlo opakující se do nekonečna. Mandelbrot zjistil, že pro určité hodnoty komplexních čísel roste vzorec do nekonečna, ale pro jiné klesají k nule.  

Ukážeme si to na příkladu. Uvažujme komplexní číslo c = 1. Začínáme s hodnotou z=0 a v každém dalším kroku zvolíme hodnotu z jako tu, která nám vyšla z předchozího výpočtu:

Z₀=0² + 1=1 

Z₁=1² + 1 = 2 

Z₂=2² + 1 = 5 

Z₅=5² + 1 = 25...

… zde vidíme, že pro hodnotu komplexního čísla c = 1 výsledek limitně blíží nekonečnu. Číslo 1 tedy nepatří do Mandelbrotovi množiny.  

Zkusme teď komplexní číslo c = -1 

Z₀= 0² –1 = -1 

Z-₁= (-1)² – 1 = 0 

Z₀= 0² –1 = -1...

..zde nám hodnota přeskakuje neustále mezi –1 a 0, neuteče nám do nekonečna a tak komplexní číslo c= -1 je součástí Mandelbrotovi množiny.  

Když tento výpočet provedeme pro všechna komplexní čísla a ta, která nám “neutekla” do nekonečna nakreslíme do grafu, dostaneme Mandelbrotovu množinu. Vně se nacházejí hodnoty z rostoucí do nekonečna, uvnitř jsou uvězněny ty odsouzené k zániku, a tedy směřují k nule. Bez ohledu na to, jak obrázek přiblížíme, uvidíme podobné tvary a nebudeme se moci dostat ke konečnému bodu. Tvary se budou neustále opakovat.

Každý objekt má fraktální dimenzi, která je druhem statistické „míry drsnosti“. Brokolice má fraktální dimenzi kolem 2,8, pobřeží 1,28 a lidské plíce mají kolem 2,97. Celý náš svět je dokonalá, složitá geometrie. Když se podíváme na nějaký objekt, zdá se nám nematematický, protože vidíme celou jeho složitost. Když se pozorně podíváme na to, z jakých tvarů se skládá, můžeme vidět trojrozměrnou geometrii neustále se opakujících, soběpodobných objektů. Vzorce pro stromy, mraky a horská pásma se mohou vytvářet zcela uměle na základě míry jejich komplexnosti. Vědci také hledají fraktální vzorce v množinách dat, které se jinak mohou jevit jako chaotické. Po objevení fraktální geometrie se zlepšila počítačová grafika a grafika ve filmech. Můžeme si všimnout, že se zlepšili objekty v počítačových hrách, krajiny jsou více realistické, protože k jejich vykreslení se používá počítačem generovaná grafika (CGI). Pomocí fraktální geometrie bylo umožněno správně měřit velikosti pobřeží, pohyby mraků, změny v korytech řek, antény zmenšili své rozměry, zvětšil se rozsah rádiových vln. V informatice se fraktály používají ke zmenšení objemu přenesených dat, kompresy dat a kompaktnímu ukládání informací.  Fraktály se používají i v jaderné fyzice a astrofyzice při studiu elementárních částic, slunečních procesů a rozložení galaxií ve vesmíru. Fraktální geometrie umožňuje předpovídat infarkty, diagnostikovat ranná stádia rakoviny. Dokonce i pohyb Braunových částic, který byl dřív považován za chaotické, v sobě také skrývá fraktální geometrii. Zdánlivý chaos ve vesmíru skrývá dokonalý řád.  

Celý náš svět, je nejsložitější geometrií, která je uložena jak ve vnějším zobrazení našeho světa, tak v základu jeho vzniku a ve složitých fyzikálních procesech. 

Připomeňme si, že každá část soběpodobného tvaru, ať už se na ni díváme v jakémkoliv měřítku, připomíná celek. V tomto ohledu splňuje vykreslení Mandelbrotovi množiny definici soběpodobnosti dokonale.   

iQTIP:

Peanova křivka 

Roku 1890 objevil Ital Giuseppe Peano jednodimenzionální křivku, která se může neustále rozvíjet na dvojrozměrné ploše. Peano použil konstrukci podobnou Kochově křivce, ale předem vypočítanou. Začal se zobrazením jednotky intervalu v daném čtverci a proces opakoval s menšími intervaly. Vytvořil nekonečně dlouhou čáru, která nepřesahuje daný čtverec. Peano ve skutečnosti nikdy křivku nenarýsoval, dával přednost matematickému ověření této kontraintuitivní vlastnosti.