Zlatý řez – propojení matematiky a estetiky aneb „božský poměr"

Astronom Johannes Kepler prohlásil: „Geometrie má dva poklady. Jeden z nich je Pythagorova věta a druhý zlatý řez. První má cenu zlata, druhý připomíná spíše drahocenný kámen.“ 

Zlatým řezem je číslo a matematicky jde o řešení rovnice: 

x2 – x – 1 = 0  (x= 1,61803398874….),  což lze zaznamenat jako:  x/1 = 1/(x-1).  Vyjádřeno slovy:  „Zlatý řez je poměr, při kterém se celá část má k větší tak, jak se má větší část k menší.“

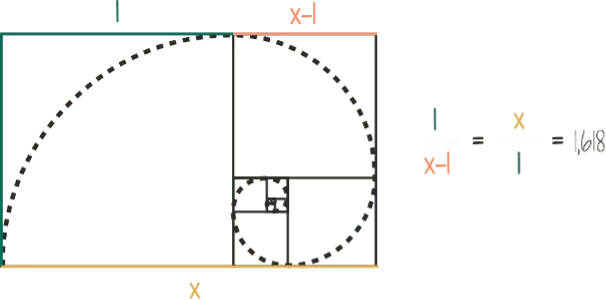
Hodnota tohoto poměru 1,618 : 1 (nebo 1 : 0,618) je rovna iracionálnímu číslu. 

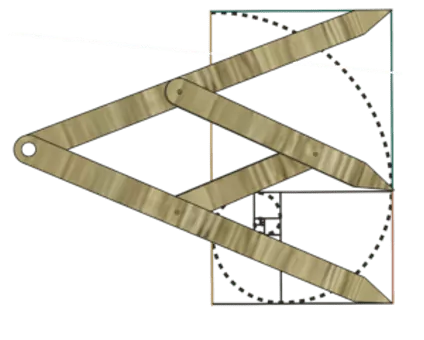
Úžasné a tajemné na zlatém řezu je, že vedle matematiky a věcí vytvořených člověkem (architektur, kreditních karet, vitruviově figuře), se objevuje v přírodě: v botanice, zoologii či krystalografii.  

Abychom lépe pochopili vlastnosti zlatého řezu, musíme se seznámit s Fibonacciho posloupností. 

Fibonacciho posloupnost

Fibonacciho posloupnost patří mezi nejznámější posloupnosti, označuje se jí nekonečná řada čísel 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89 …. 

Je pojmenována po Leonardu Pisánském (přezdívalo se mu Fibonacci), který žil na přelomu 12. a 13. století v Itálii. Každé číslo v této posloupnosti je součtem dvou předchozích čísel, takže například: 

2 = 1 + 1 ; 3 = 1 + 2 ; 5 = 2 + 3 a tak dále. Členy této posloupnosti také nazýváme jako Fibonacciho čísla. 

Pokud postupně sestrojíme čtverce o stranách s délkami rovnými Fibonacciho číslům 1, 1, 2, 3, 5, 8, 13, 21, 34…, tak je možné je hezky poskládat vedle sebe. Pokud načrtneme v každém z nich čtvrtkružnici, tak nám vznikne Fibonacciho spirála. 

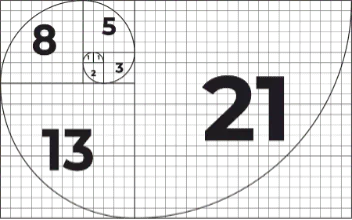
Limita poměru dvou následujících čísel Fibonacciho posloupnosti je rovna zlatému řezu, či-li blíží se hodnotě 1,618….. 

Fibonacciho čísla figurují ve spirálovitých strukturách na povrchu šišek jehličnanů či ananasu, v terči slunečnice, sedmikrásky a jiných květů. Na uvedených rostlinách je možné pozorovat dva systémy spirál. Spirály levotočivé a pravotočivé. Počty spirál v obou směrech vždy odpovídají velikosti rostliny, nebo se dají vyjádřit sousedními členy Fibonacciho posloupnosti.  Například u slunečnice je nejčastěji jedním směrem 34 spirál a druhým směrem 55 spirál. 

Zajímavostí je sledovat počet okvětních lístků květů různých rostlin. Velmi časté jsou květy, jejichž počet okvětních plátků je nějakým Fibonacciho číslem.  Příklady: 1 plátek: kala, anturie, 2 plátky: euforbia, 3 plátky: kosatec, 5 plátků: pomněnka, 8 plátků: celandine, 13 plátků: třepatka, 21 plátků: čekanka, 34 plátků: kopretina. 

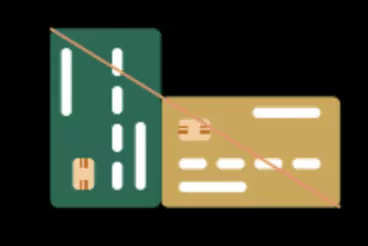
Dobrým příkladem použití zlatého řezu v běžném životě je kreditní karta, jejíž velikost je celosvětově standardizována a je v souladu s definicí zlatého řezu. Kreditní karta má tvar tzv. zlatého obdélníku (jeho strany jsou v poměru zlatého řezu). Zlatý obdélník je oblíbený tvar díky jeho vyváženému vzhledu – není ani příliš dlouhý ani příliš široký. 

Fibonacciho čísla se často vyskytují tamtéž, kde potkáváme i zlatý řez. Obdélníky, s nimiž se setkáme při výstavbě čtvercové spirály, jsou k nerozeznání od zlatých obdélníků. 

Jak zjistit, že je obdélník zlatý? 

Polož dva stejné obdélníky vedle sebe: jeden na výšku, druhý vedle něj na šířku. Pokud přeložíš úhlopříčku na šířku položeným obdélníkem a ta dosáhne horního vrcholu druhého obdélníku, pak jsou oba zlaté.

Ať už zlatý řez vyjádříme jakkoli, vždy má v sobě jistou jednoduchost a šarm.