Pí, Pí, Pí a zase Pí

My ale chceme pohled na matematiku změnit. A to ne proto, abyste rozuměli matematickým meme na instagramu, ale abyste třeba neprohloupili a neprodělali.

V posledních letech roste obliba rozvozu hotových jídel. Situace kolem onemocnění COVID-19 vše ještě umocnila. Mezi moje oblíbená jídla, když už sáhnu po rozvozu, patří pizza. Jednak si ji doma sám neudělám, a jednak mi opravdu moc chutná.

Ale není těch peněz za pizzu někdy moc? Je lepší objednat si jednu velkou pizzu, nebo dvě malé? Co je výhodnější?

Pizza je vlastně válec. Ano, ne kruh, ale válec, protože má i nějakou tloušťku. Já miluji mnemotechnické pomůcky všeho druhu a jedna moje oblíbená na výpočet objemu válce souvisí právě s pizzou. Než se k ní ale dostaneme, připomeňme si číslo Pí, které budeme k výpočtu potřebovat.

Číslo Pí, nazýváno také jako Ludolfovo číslo, udává, kolikrát je obvod kruhu větší než jeho průměr. Velmi jednoduchá, ale dokonalá definice.

Číslo Pí se využívá v desítkách rovnic a většina z nás zná jeho přibližnou hodnotu jako 3,14. Číslo Pí má svůj den 14. 3. (protože v anglosaských zemích se datum píše jako 3.14).

V Evropě by se měl slavit evropský den Pí 22. 7., protože hodnota zlomku 22/7 = 3,14285 má skutečné hodnotě čísla Pí blíže než amerických 3,14.

“Pí”ramidy?

Poměr obvodu k výšce Velké pyramidy činí 22:7, čili 3,142. Všechny pyramidy v Gíze mají poměr obvodu k výšce velmi blízký hodnotě Pí. Lze jen spekulovat, jestli stavitelé měli své výpočty založené na Pí, nebo jen měli z nějakého důvodu tento poměr v oblibě.

Archimedes, nebo Ludolf?

Číslo Pí však nekončí s pár čísly za desetinnou čárkou, ale má nekonečný desetinný rozvoj (je iracionální). Stanovit jej co nejpřesněji jako první zkoušel Archimedes. Ten postupoval tak, že kružnici vepisoval a opisoval mnohoúhelníky. Počet jejich stran neustále zvyšoval, a tím se tak stále více a více přibližoval tvaru kružnice, a tím tak i zpřesňoval výpočet čísla Pí. Lidem tento postup stačil asi 2000 let. Stejný postup jako Archimedes použil i holandský matematik Ludolph van Ceulen (1540-1610), který přibližně 25 let svého života trávil počítáním čísla Pí. Pomocí pravidelného 4 611 686 018 427 387 904-úhelníka dopočítal číslo Pí na 35 desetinných míst (nicméně později se přišlo na to, že dvě číslice měl chybně).  Na jeho počest se však číslo Pí nazývá také jako Ludolfovo číslo. Za to, že svůj život obětoval výpočtu čísla Pí, má číslo Pí s jeho objevenými 35 místy za desetinnou čárkou vytesáno na náhrobku.

S objevením infinitezimálního počtu (integrálů) se namísto Archimedova náročného postupu začínají hledat vzorce na výpočet Pí (značeno π) pomocí částečných součtů rozvojů nekonečných řad. Matematici Pí neustále zpřesňují, v roce 2007 bylo vypočítáno na 2,7 bilionů desetinných míst.

Rekord v zapamatování si co největšího počtu desetinného rozvoje čísla Pí drží Suresh Kumar Sharma, který si číslo Pí zapamatoval na neuvěřitelných 77 000 desetinných míst.

V reálném světě se však tolik desetinných míst nepoužívá. Pro výpočty meziplanetárních letů používá NASA 15 desetinných míst. Čtyřicetimístná hodnota Pí stačí na to, aby se mohl vypočítat průměr celého známého vesmíru natolik přesně, že stupeň nepřesnosti by byl menší, než je číselná velikost atomu vodíku. Sami jistě uznáte, že běžnému člověku stačí k zapamatování několik číslic rozvoje čísla Pí. Pomoci nám mohou tzv. piemy. To jsou literární útvary pro zapamatování si čísla Pí. Počet písmen každého slova koresponduje s hodnotou číslice na příslušném místě:

Dej, ó bože, ó mocný, pamatovat si takový cifer řad, velký slovutný Archimede, pomáhej trápenému! (3,14159265358979)

Lín a kapr u hráze prohlídli si rybáře, udici měl novou, jikrnáči neuplavou.

(3,  1   4    1     5           9        2       6         5       3        5          8             9 )

Teď ale zpět k pizze a číslu Pí. Stojí před námi problém. Je výhodnější koupit dvě malé pizzy za 338 Kč, nebo raději jednu velkou za 259 Kč? Začíná jít do tuhého, pokud jde o jídlo a naše peníze.

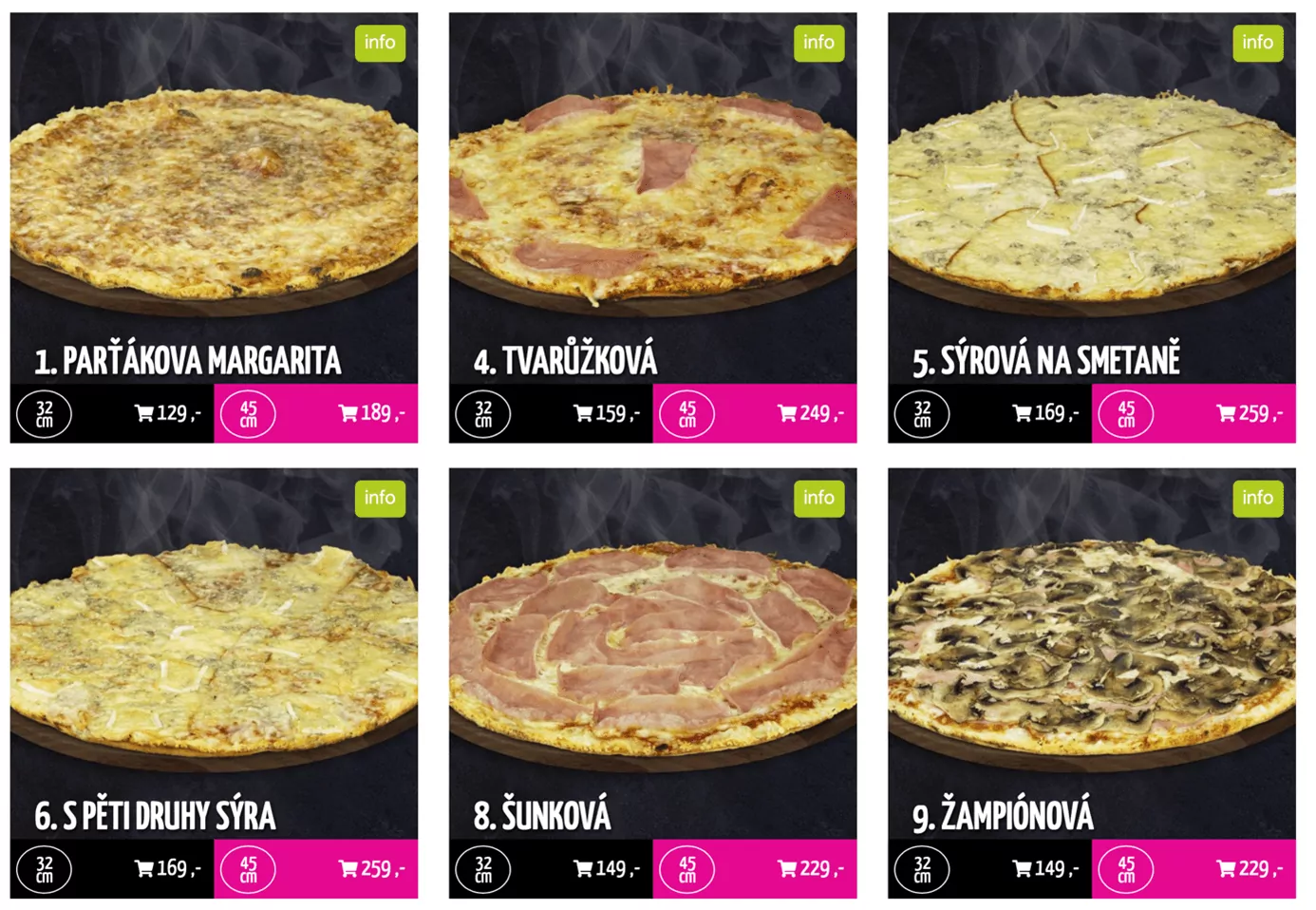
Budeme předpokládat, že obě pizzy (malá i velká) mají stejnou tloušťku a zjednodušíme si výpočet jen na zjištění obsahu kruhu. A to bez Pí prostě nejde. Vzoreček i výpočet jsou jednoduché: 

S = π*r² (S = obsah pizzy, r = rádius = poloměr pizzy)

Malá pizza je asi 32 cm² (S=3,1415*0,32² = 0,3216 m²)

Velká pizza je asi 64 cm² (S=3,1415*0,45² = 0,6361 m²)

Co z toho plyne? Velká pizza má přesně dvakrát větší obsah než ta malá. Takže se vyplatí koupit jednu velkou než dvě malé. Kromě toho se také vyplatí umět matematiku!

A jestli Vás doteď matematika nebavila, můžete se těšit. V iQLANDII právě chystáme nový projekt, jehož prostřednictvím si matematiku „osaháte“ a lépe ji pochopíte.

A ještě slibovaná mnemotechnická pomůcka pro zapamatování si výpočtu objemu (anglicky Volume) válce pomocí pizzy.
​​​